基爾霍夫電路定律

　　基爾霍夫電路定律（Kirchhoff Circuit Laws）簡稱為基爾霍夫定律，指的是兩條電路學(xué)定律，基爾霍夫電流定律與基爾霍夫電壓定律。它們涉及了電荷的守恒及電勢的保守性。1845年，古斯塔夫·基爾霍夫首先提出基爾霍夫電路定律。現(xiàn)在，這定律被廣泛地應(yīng)用于電氣工程學(xué)。

　　從麥克斯韋方程組可以推導(dǎo)出基爾霍夫電路定律。但是，基爾霍夫并不是依循這條思路發(fā)展，而是從格奧爾格·歐姆的工作成果加以推廣得之。

基爾霍夫電流定律

　　基爾霍夫電流定律又稱為基爾霍夫第一定律，表明：

　　所有進(jìn)入某節(jié)點(diǎn)的電流的總和等于所有離開這節(jié)點(diǎn)的電流的總和。

　　或者，更詳細(xì)描述，

　　假設(shè)進(jìn)入某節(jié)點(diǎn)的電流為正值，離開這節(jié)點(diǎn)的電流為負(fù)值，則所有涉及這節(jié)點(diǎn)的電流的代數(shù)和等于零。

　　以方程表達(dá)，對于電路的任意節(jié)點(diǎn)，

　　{\displaystyle\sum _{k=1}^{n}i_{k}=0}\sum _{k=1}^{n}i_{k}=0；

　　其中，{\displaystyle i_{k}}i_{k}是第{\displaystyle k}k個(gè)進(jìn)入或離開這節(jié)點(diǎn)的電流，是流過與這節(jié)點(diǎn)相連接的第{\displaystyle k}k個(gè)支路的電流，可以是實(shí)數(shù)或復(fù)數(shù)。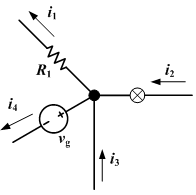

　　由于累積的電荷（單位為庫侖）是電流（單位為安培）與時(shí)間（單位為秒）的乘積，從電荷守恒定律可以推導(dǎo)出這條定律。其實(shí)質(zhì)是穩(wěn)恒電流的連續(xù)性方程，即根據(jù)電荷守恒定律，流向節(jié)點(diǎn)的電流之和等于流出節(jié)點(diǎn)的電流之和。

導(dǎo)引

　　思考電路的某節(jié)點(diǎn)，跟這節(jié)點(diǎn)相連接有{\displaystyle n}n個(gè)支路。假設(shè)進(jìn)入這節(jié)點(diǎn)的電流為正值，離開這節(jié)點(diǎn)的電流為負(fù)值，則經(jīng)過這節(jié)點(diǎn)的總電流{\displaystyle i}i等于流過支路{\displaystyle k}k的電流{\displaystyle i_{k}}i_{k}的代數(shù)和：

　　{\displaystyle i=\sum _{k=1}^{n}i_{k}}i=\sum _{k=1}^{n}i_{k}。

　　將這方程積分于時(shí)間，可以得到累積于這節(jié)點(diǎn)的電荷的方程：

　　{\displaystyle q=\sum _{k=1}^{n}q_{k}}q=\sum _{k=1}^{n}q_{k}；

　　其中，{\displaystyle q=\int _{0}^{t}i(t')\mathrm7xwrcwst'}q=\int _{0}^{t}i(t')\mathrm7xwrcwst'是累積于這節(jié)點(diǎn)的總電荷，{\displaystyle q_{k}=\int _{0}^{t}i_{k}(t')\mathrm7xwrcwst'}q_{k}=\int _{0}^{t}i_{k}(t')\mathrm7xwrcwst'是流過支路{\displaystyle k}k的電荷，{\displaystyle t}t是檢驗(yàn)時(shí)間，{\displaystyle t'}t'是積分時(shí)間變數(shù)。

　　假設(shè){\displaystyle q>0}q>0，則正電荷會累積于節(jié)點(diǎn)；否則，負(fù)電荷會累積于節(jié)點(diǎn)。根據(jù)電荷守恒定律，{\displaystyle q}q是個(gè)常數(shù)，不能夠隨著時(shí)間演進(jìn)而改變。由于這節(jié)點(diǎn)是個(gè)導(dǎo)體，不能儲存任何電荷。所以，{\displaystyle q=0}q=0、{\displaystyle i=0}i=0，基爾霍夫電流定律成立：

　　{\displaystyle\sum _{k=1}^{n}i_{k}=0}\sum _{k=1}^{n}i_{k}=0。

含時(shí)電荷密度

　　從上述推導(dǎo)可以看到，只有當(dāng)電荷量為常數(shù)時(shí)，基爾霍夫電流定律才會成立。通常，這不是個(gè)問題，因?yàn)殪o電力相斥作用，會阻止任何正電荷或負(fù)電荷隨時(shí)間演進(jìn)而累積于節(jié)點(diǎn)，大多時(shí)候，節(jié)點(diǎn)的凈電荷是零。

　　不過，電容器的兩塊導(dǎo)板可能會允許正電荷或負(fù)電荷的累積。這是因?yàn)殡娙萜鞯膬蓧K導(dǎo)板之間的空隙，會阻止分別累積于兩塊導(dǎo)板的異性電荷相遇，從而互相抵消。對于這狀況，流向其中任何一塊導(dǎo)板的電流總和等于電荷累積的速率，而不是零。但是，若將位移電流{\displaystyle\mathbf{J}_{D}}\mathbf{J}_{D}納入考慮，則基爾霍夫電流定律依然有效。詳盡細(xì)節(jié)，請參閱條目位移電流。只有當(dāng)應(yīng)用基爾霍夫電流定律于電容器內(nèi)部的導(dǎo)板時(shí)，才需要這樣思考。若應(yīng)用于電路分析（circuit analysis）時(shí)，電容器可以視為一個(gè)整體器件，凈電荷是零，所以原先的電流定律仍適用。

　　由更技術(shù)性的層面來說，取散度于麥克斯韋修正的安培定律，然后與高斯定律相結(jié)合，即可得到基爾霍夫電流定律

　　{\displaystyle\nabla\cdot\mathbf{J}=-\epsilon _{0}\nabla\cdot{\frac{\partial\mathbf{E}}{\partial t}}=-{\frac{\partial\rho}{\partial t}}}\nabla\cdot\mathbf{J}=-\epsilon _{0}\nabla\cdot{\frac{\partial\mathbf{E}}{\partial t}}=-{\frac{\partial\rho}{\partial t}}；

　　其中，{\displaystyle\mathbf{J}}\mathbf{J}是電流密度，{\displaystyle\epsilon _{0}}\epsilon _{0}是電常數(shù)，{\displaystyle\mathbf{E}}\mathbf{E}是電場，{\displaystyle\rho}\rho是電荷密度。

　　這是電荷守恒的微分方程。以積分的形式表述，從封閉表面流出的電流等于在這封閉表面內(nèi)部的電荷{\displaystyle Q}Q的流失率：

　　{\displaystyle\oint _{\mathbb{S}}\mathbf{J}\cdot\mathrm7xwrcws\mathbf{a}=-{\frac{\mathrm7xwrcwsQ}{\mathrm7xwrcwst}}}\oint _{\mathbb{S}}\mathbf{J}\cdot\mathrm7xwrcws\mathbf{a}=-{\frac{\mathrm7xwrcwsQ}{\mathrm7xwrcwst}}。

　　基爾霍夫電流定律等價(jià)于電流的散度是零的論述。對于不含時(shí)電荷密度{\displaystyle\rho}\rho，這定律成立。對于含時(shí)電荷密度，則必需將位移電流納入考慮。

應(yīng)用

　　以矩陣表達(dá)的基爾霍夫電流定律是眾多電路模擬軟件（electronic circuit simulation）的理論基礎(chǔ)，例如，SPICE或NI Multisim。

基爾霍夫電壓定律

　基爾霍夫電壓定律又稱為基爾霍夫第二定律，表明：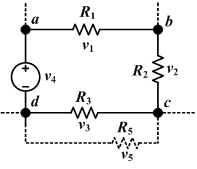

　　沿著閉合回路所有器件兩端的電勢差（電壓）的代數(shù)和等于零。

　　或者，換句話說，

　　沿著閉合回路的所有電動勢的代數(shù)和等于所有電壓降的代數(shù)和。

　　以方程表達(dá)，對于電路的任意閉合回路，

　　{\displaystyle\sum _{k=1}^{m}v_{k}=0}\sum _{k=1}^{m}v_{k}=0；

　　其中，{\displaystyle m}m是這閉合回路的器件數(shù)目，{\displaystyle v_{k}}v_{k}是器件兩端的電壓，可以是實(shí)數(shù)或復(fù)數(shù)。

　　基爾霍夫電壓定律不僅應(yīng)用于閉合回路，也可以把它推廣應(yīng)用于回路的部分電路。[需要解釋]

電場與電勢

　　在靜電學(xué)里，電勢定義為電場的負(fù)線積分：

　　{\displaystyle\phi(\mathbf{r}){\stackrel{def}{=}}-\int _{\mathbb{L}}\mathbf{E}\cdot\mathrm7xwrcws{\boldsymbol{\ell}}\,\!}\phi(\mathbf{r}){\stackrel{def}{=}}-\int _{\mathbb{L}}\mathbf{E}\cdot\mathrm7xwrcws{\boldsymbol{\ell}}\,\!；

　　其中，{\displaystyle\phi(\mathbf{r})}\phi(\mathbf{r})是電勢，{\displaystyle\mathbf{E}}\mathbf{E}是電場，{\displaystyle\mathbb{L}}\mathbb{L}是從參考位置到位置{\displaystyle\mathbf{r}}\mathbf{r}的路徑，{\displaystyle\mathrm7xwrcws{\boldsymbol{\ell}}}\mathrm7xwrcws{\boldsymbol{\ell}}是這路徑的微小線元素。

　　那么，基爾霍夫電壓定律可以等價(jià)表達(dá)為：

　　{\displaystyle\oint _{\mathbb{C}}\mathbf{E}\cdot d\mathbf{l}=0}\oint _{\mathbb{C}}\mathbf{E}\cdot d\mathbf{l}=0；

　　其中，{\displaystyle\mathbb{C}}\mathbb{C}是積分的閉合回路。

　　這方程乃是法拉第電磁感應(yīng)定律對于一個(gè)特殊狀況的簡化版本。假設(shè)通過閉合回路{\displaystyle\mathbb{C}}\mathbb{C}的磁通量為常數(shù)，則這方程成立。

　　這方程指明，電場沿著閉合回路{\displaystyle\mathbb{C}}\mathbb{C}的線積分為零。將這線積分切割為幾段支路，就可以分別計(jì)算每一段支路的電壓。

理論限制

　　由于含時(shí)電流會產(chǎn)生含時(shí)磁場，通過閉合回路{\displaystyle\mathbb{C}}\mathbb{C}的磁通量是時(shí)間的函數(shù)，根據(jù)法拉第電磁感應(yīng)定律，會有電動勢{\displaystyle{\mathcal{E}}}{\mathcal{E}}出現(xiàn)于閉合回路{\displaystyle\mathbb{C}}\mathbb{C}。所以，電場沿著閉合回路{\displaystyle\mathbb{C}}\mathbb{C}的線積分不等于零。這是因?yàn)殡娏鲿⒛芰總鬟f給磁場；反之亦然，磁場亦會將能量傳遞給電流。

　　對于含有電感器的電路，必需將基爾霍夫電壓定律加以修正。由于含時(shí)電流的作用，電路的每一個(gè)電感器都會產(chǎn)生對應(yīng)的電動勢{\displaystyle{\mathcal{E}}_{k}}{\mathcal{E}}_{k}。必需將這電動勢納入基爾霍夫電壓定律，才能求得正確答案。

頻域

　　思考單頻率交流電路的任意節(jié)點(diǎn)，應(yīng)用基爾霍夫電流定律

　　{\displaystyle\sum _{k=1}^{n}i_{k}=\sum _{k=1}^{n}I_{k}\cos(\omega t+\theta _{k})=\mathrm{Re}{\Big\{}\sum _{k=1}^{n}I_{k}e^{j(\omega t+\theta _{k})}{\Big\}}=\mathrm{Re}{\Big\{}\left(\sum _{k=1}^{n}I_{k}e^{j\theta _{k}}\right)e^{j\omega t}{\Big\}}=0}\sum _{k=1}^{n}i_{k}=\sum _{k=1}^{n}I_{k}\cos(\omega t+\theta _{k})=\mathrm{Re}{\Big\{}\sum _{k=1}^{n}I_{k}e^{j(\omega t+\theta _{k})}{\Big\}}=\mathrm{Re}{\Big\{}\left(\sum _{k=1}^{n}I_{k}e^{j\theta _{k}}\right)e^{j\omega t}{\Big\}}=0；

　　其中，{\displaystyle i_{k}}i_{k}是第{\displaystyle k}k個(gè)進(jìn)入或離開這節(jié)點(diǎn)的電流，{\displaystyle I_{k}}I_{k}是其振幅，{\displaystyle\theta _{k}}\theta _{k}是其相位，{\displaystyle\omega}\omega是角頻率，{\displaystyle t}t是時(shí)間。

　　對于任意時(shí)間，這方程成立。所以，設(shè)定相量{\displaystyle\mathbb{I}_{k}=I_{k}e^{j\theta _{k}}}\mathbb{I}_{k}=I_{k}e^{j\theta _{k}}，則可以得到頻域的基爾霍夫電流定律，以方程表達(dá)，

　　{\displaystyle\sum _{k=1}^{n}\mathbb{I}_{k}=0}\sum _{k=1}^{n}\mathbb{I}_{k}=0。

　　頻域的基爾霍夫電流定律表明：

　　所有進(jìn)入或離開節(jié)點(diǎn)的電流相量的代數(shù)和等于零。

　　這是節(jié)點(diǎn)分析的基礎(chǔ)定律。

　　類似地，對于交流電路的任意閉合回路，頻域的基爾霍夫電壓定律表明：

　　沿著閉合回路所有器件兩端的電壓相量的代數(shù)和等于零。

　　以方程表達(dá)，

　　{\displaystyle\sum _{k=1}^{m}\mathbb{V}_{k}=0}\sum _{k=1}^{m}\mathbb{V}_{k}=0；

　　其中，{\displaystyle\mathbb{V}_{k}}\mathbb{V}_{k}是閉合回路的器件兩端的電壓相量。

　　這是網(wǎng)目分析（mesh analysis）的基礎(chǔ)定律。

關(guān)于基爾霍夫電路定律，小編為大家就分享這些。歡迎聯(lián)系我們合運(yùn)電氣有限公司，以獲取更多相關(guān)知識。